Jogadores de RPG mais veteranos sabem que embora haja uma miríade de sistemas diferentes, na verdade o número de bases para um sistema de jogo (estamos falando da parte matemática das regras aqui) é bastante restrito.

Desses sistemas básicos podemos citar dois principais: os que usam 1d20 para resolver a maior parte das ações (caso de D&D, AD&D, D&D 4ª Edição, D&D 5ª Edição, D20, etc… Aqui também se encaixa 3D&T, como veremos adiante) e o sistema 3d6 (GURPS, ….).

Da mesma forma é bem normal que sistemas de RPG tenham os conceitos de “Falha Crítica” (quando você tira um resultado muito baixo nos dados) e “Sucesso Decisivo” – ou “Acerto Crítico” – que é quando você tira um resultado muito alto nos dados.

Antes de prosseguir, é interessante citar que utilizaremos aqui alguns conceitos de matemática (sim, aquela matéria “chata”), mas apenas conteúdos referentes ao ensino médio, mais especificamente de análise combinatória.

Caso não tenha espantado nenhum de vocês, vamos em frente.

1d20 – Probabilidade linear

Aqui as coisas ainda são fáceis.  A pergunta que temos que responder é:

“Quando eu jogo 1d20, qual a probabilidade de dar 1?”

Jogando 1d20 há exatamente 20 possibilidades de resultado: justamente os números de 1 a 20. Como estamos jogando apenas um dado a probabilidade de termos qualquer resultado é exatamente a mesma. A chance de sair 1, ou 20, ou 10 é exatamente igual. No caso específico de 1d20 a chance é (dã!) uma em vinte.

Desse modo podemos montar uma tabela com todos os resultados possíveis, todas as combinações de dados que podem dar aquele resultado (essa coluna ainda não faz muito sentido. Confiem no Ghost. Mais algusn parágrafos e fará) e a probabilidade de sair aquele resultado.

Resultado	Combinações	Chance
1	1	5%
2	1	5%
3	1	5%
4	1	5%
5	1	5%
6	1	5%
7	1	5%
8	1	5%
9	1	5%
10	1	5%
11	1	5%
12	1	5%
13	1	5%
14	1	5%
15	1	5%
16	1	5%
17	1	5%
18	1	5%
19	1	5%
20	1	5%
TOTAL	20	100%

Essa tabela quer dizer que há apenas uma possibilidade de cada resultado quando jogamos 1d20, e a chance de cada resultado aparecer é de 5% (100% dividido pelas 20 “combinações” possíveis).

Transformando essa tabela em um gráfico (gráficos são sempre mais fáceis de visualizar), temos uma imagem bem boring.

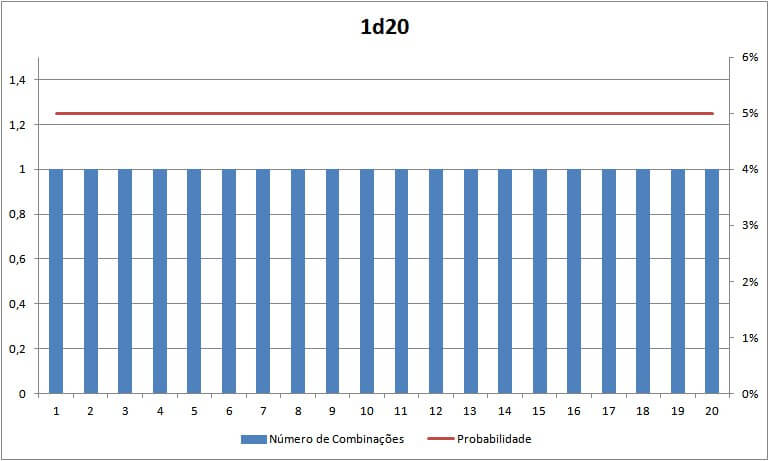
Isso se chama “Probabilidade Linear”, quando a chance de qualquer resultado é exatamente a mesma.

Guardem essas informações. Voltaremos a elas em alguns minutos.

Todos os sistemas que utilizam apenas um dado para os testes (incluindo 3D&T) caem em um caso semelhante.

3d6 – Probabilidade Gaussiana

Quando jogamos 3d6, entretanto, a coisa é bem diferente. Há apenas uma combinação que gera o resultado 3 (todos os dados darem 1), e apenas uma combinação que gera o resultado 18 (todos os dados darem 6).

Um resultado 4, por outro lado, pode aparecer de três maneiras diferentes:

1	1	2
1	2	1
2	1	1

Dessa forma um resultado 4 é três vezes mais provável do que um resultado 3.

Seguindo o mesmo raciocínio, combinando os dados de todas as formas possíveis, chegamos nessa tabela de resultados (vamos manter de 1 a 20 para facilitar a comparação):

Resultado	Combinações	Chance
1	0	0,00%
2	0	0,00%
3	1	0,46%
4	3	1,39%
5	6	2,78%
6	10	4,63%
7	15	6,94%
8	21	9,72%
9	25	11,57%
10	27	12,50%
11	27	12,50%
12	25	11,57%
13	21	9,72%
14	15	6,94%
15	10	4,63%
16	6	2,78%
17	3	1,39%
18	1	0,46%
19	0	0,00%
20	0	0.00%
TOTAL	216	100%

Existe um total de 216 combinações diferentes quando jogamos 3 dados de 6 faces (6 resultados possíveis para o primeiro dado vezes 6 resultados possíveis para o segundo vezes 6 resultados possíveis para o terceiro: 6x6x6 = 216).

Transformando esses números em um gráfico temos o que é chamado de probabilidade “normal” (ou “Gaussiana”, em homenagem ao matemático alemão Johann Carl Friedrich Gauss, o primeiro a descrever esse tipo de curva).

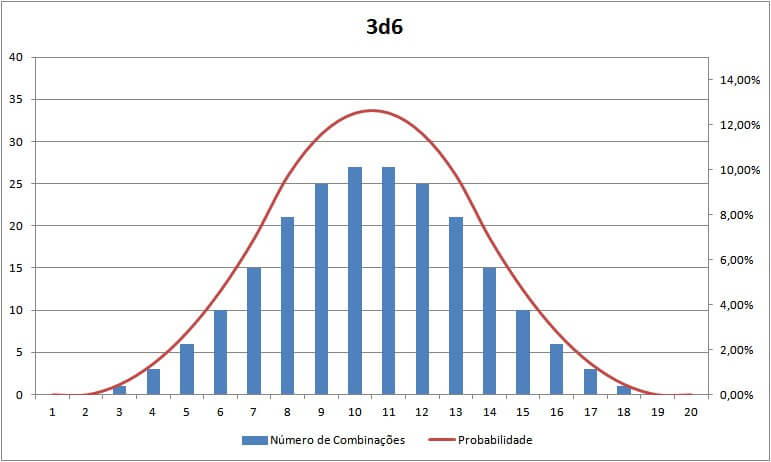
Isso altera drasticamente a distribuição dos resultados, já que a probabilidade de cada resultado sair é calculada pelo número de jogadas que dão aquele resultado (a coluna que comentei que ainda não fazia muito sentido, mas agora faz) dividido pelo número total de combinações (216, no caso).

O ponto de atenção aqui é: quando jogamos 1d20 em 10% das jogadas obtemos um resultado 1 OU 20 (falha crítica ou sucesso decisivo). De cada dez vezes em que o personagem tenta algo, uma delas resulta em sucesso decisivo ou falha crítica.

Quando jogamos 3d6, por outro lado, as chances de obter um 3 OU 18 são de apenas 0,9% ou menos de uma vez a cada 100 jogadas!

E resultados medianos? Considerando que um resultado mediano é a faixa de 9 a 12, a chance de obter um resultado nesse intervalo é de 20% no 1d20 (5% + 5% + 5% + 5%), mas impressionantes 48,15% quando jogamos 3d6 (11,57% + 12,50% +12,50% +11,57%).

Tá! E daí?!?

Ocorre que a distribuição Gaussiana é muito mais comum no mundo real do que a linear, especialmente quando descrevemos algo como  “capacidade de uma pessoa de fazer alguma coisa”.

Por exemplo: se você juntar aleatoriamente mil pessoas e pedir para que elas corram 100 m no menor tempo que conseguirem, você vai ter um número imenso de pessoas percorrendo a distância em, digamos, entre 25 e 35 segundos, mas talvez ninguém consiga fazê-lo em menos de 10s (tempo reservado a alguns velocistas olímpicos), e possivelmente ninguém (em boas condições físicas) levará mais do que um minuto.

E em termos de jogo? Em termos de jogo isso quer dizer que em sistemas 3d6 o sucesso (ou falha) crítico deveria ser BEM mais valorizado do que no 1d20. Se um personagem de GURPS tira 3 (o melhor resultado possível, o efeito deveria ser nada menos que ÉPICO dentro das circunstâncias). Já no caso do 1d20 não é necessário que um 20 seja algo tão marcante, já que ele ocorre com uma frequência 11 vezes maior que o 3 em 3d6. Em D&D o sucesso decisivo pode ser algo mais subjetivo, e o mestre pode flexibilizar mais os resultados, sendo uma maneira de “roubar nos dados” sem propriamente roubar.

Exemplo: um mago de nível 1 tirando 20 em uma jogada de ataque poderia ter um resultado (em termos de jogo) mais espetacular do que um bárbaro/guerreiro do mesmo nível (ou de nível mais elevado), simplesmente por que não se espera que um mago tenha um resultado tão bom em um ataque (e provavelmente ele atacará com bem menos frequência do que o bárbaro/guerreiro do grupo).

Também existem algumas maneiras de “amortecer” esse efeito no d20. Por exemplo:

• Definir que em caso de resultado “1” ou “20” existe um percentual de chance de ser um acerto ou falha crítica (50%, ou 30%, a gosto do mestre).
• Rolar 3d20 e descartar o maior e o menor resultado. Isso significa que só teremos um acerto (ou falha) crítico quando todos os três dados resultarem 1 ou 20 (o que ocorrerá apenas uma vez a cada 8 MIL (!!!!) jogadas, ou seja o resultado da ação tem a obrigação de ser ÉPICO).

Um outro efeito pouco observado é o de bônus e penalidades. Um bônus de +5 em 1d20 é alto, mas em 3d6 é imenso, já que afeta muito mais a probabilidade, devido ao formato da curva.

Da mesma forma é bem menos provável de realizar feitos épicos em sistemas 3d6, mas nesses sistemas personagens iniciantes costumam ser bem mais competentes que em sistemas 1d20 (e a evolução costuma ser mais lenta). Outro fator (esse bem menos intuitivo) é que em sistemas de probabilidade linear o grupo de personagens fica bem mais poderoso simplesmente tendo um número maior de membros, enquanto em 3d6 isso não necessariamente acontece.

Também vem daí o heroísmo de 3D&T. É como D20, mas com um número de possibilidades bem menor.

Tudo o que foi citado sobre o sistema 1d20 pode ser extrapolado para qualquer sistema que utilize apenas um dado para os testes (podemos chamar de sistemas 1D), e o que foi citado para 3D6 pode ser extrapolado para qualquer sistema que utilize um número fixo e maior do que 1 de dados para os testes.

São coisas interessantes de se ter consciência, especialmente quando o grupo joga em sistemas com mecânicas diferentes e pode tentar adaptar regras de um para outro.

Curtiu a discussão? Então comente aí embaixo (ou acesse esse link , onde o tema é tratado de forma bastante profunda).

*Optamos por não incluir sistemas baseados em jogar um número variável de dados e medir o sucesso pela quantidade de dados que ultrapassam o número alvo – Storyteller, por exemplo – por que essa mecânica adiciona um terceiro fato à probabilidade (justamente o número de dados lançado), tornando a comparação excessivamente complicada.

**A pintura que ilustra esse post é The Last Throw de Charles Robert Leslie.